Lorsque l’on veut obtenir la valeur d’une intégrale numériquement, on peut s’y prendre de différentes manières.

Certaines calculatrices graphiques sont capables de calculer explicitement l’intégrale, avec des algorithmes comme l’algorithme de Risch. Mais souvent, une bonne approximation suffit, et un calcul numérique suffisamment fin permet d’obtenir rapidement une valeur proche de celle réelle.

Calculer l’intégrale d’une fonction $f$ sur un intervalle $[a, b]$, avec $a \leq b$ revient à calculer son “aire sous la courbe”, c’est-à-dire l’aire de la surface délimitée par l’axe des abscisses et la courbe et les droites verticales d’abscisse $a$ et $b$.

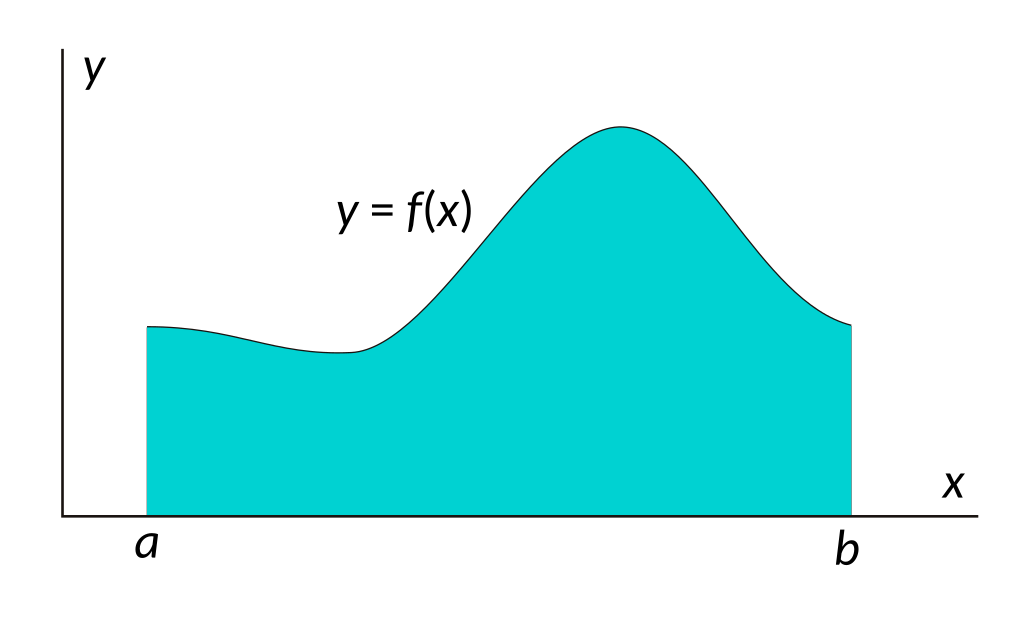
L’aire en bleu correspond ici à $$ \int_a^b f(x) \mathrm{d}x $$

On gardera cette notation dans la suite.

Méthode des rectangles

C’est la méthode classique, souvent introduite lorsqu’on parle de calcul différentiel ou de calcul infinitésimal.

L’idée est de fixer un entier $n$, puis de découper l’intervalle sur lequel on intègre en $n$ sous-intervalles de taille $\frac{1}{n}$.

On peut donc se ramener à calculer des aires plus petites, où on peut faire des approximations plus grossières : on calcule l’aire du rectangle sous la courbe sur chacun des petits sous-intervalles, comme sur le schéma suivant.

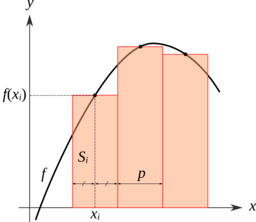
On les somme ensuite pour obtenir une approximations de l’aire globale sous la courbe, donc de la valeur de l’intégrale.

Pour cela, pour $k$ allant de $0$ à $n-1$, on doit donc choisir le point sur lequel on va calculer de la valeur de $f$ selon plusieurs choix

• à gauche du sous-intervalle $$ f(a + \frac{k}{n} \cdot (b - a)) $$
• au milieu du sous-intervalle $$ f(a + \frac{2 k + 1}{2 n} \cdot (b - a)) $$
• à la fin du sous-intervalle $$ f(a + \frac{k+1}{n} \cdot (b - a)) $$

Calculer l’aire du rectangle correspondant revient à faire le produit de sa longueur et de sa largeur, ce qui donne, si on prend le point à gauche du sous-intervalle. $$ f(a + \frac{k}{n} \cdot (b-a)) \times \frac{b-a}{n} $$

Car la longueur de chaque sous-intervalle est celle de l’intervalle initiale divisée par $n$.

L’implémentation de cette méthode est ensuite directe :

1
2
3
4
5
6
7

def calcul(f, a, b, n):
    somme = 0

    for k in range(n):
        somme += f(a  + (b - a) * k / n) * (b - a) / n

    return somme

Prenons comme exemple $$ \int_0^\pi \sin(t) \mathrm{d}t $$

Une primitive de $t \mapsto \sin(t)$ est $t \mapsto - \cos(t)$ donc $$ \int_0^\pi \sin(t) \mathrm{d}t = [-\cos(t)]_0^\pi = - (-1) + 1 = 2 $$

Cette fonction nous donne comme approximation, 1.98 pour $n = 10$ et 1.9998 pour $n = 100$.

1

print(calcul(lambda x: sin(x), 0, pi, 10))

Ça semble pas trop mal !

Méthode des trapèzes

Cette méthode est similaire à la première, mais peut permettre de légèrement mieux approximer des fonctions.

En effet, les rectangles que nous construisons font des sortes de sauts, et ne correspondent pas exactement à l’allure générale de certaines fonctions (comme les fonction polynomiales par exemple).

Une légère variation consiste donc à calculer l’aire du trapèze sous la courbe au lieu de celle du rectangle (le trapèze en question a subit une rotation, ses côtés parallèles sont ceux à droite et à gauche).

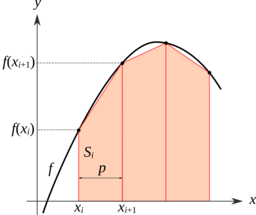
Mais reste à connaître la formule de l’aire d’un trapèze ! La formule du trapèze est la suivante, avec $a$ et $c$ les longueurs des côtés parallèles, et $h$ la hauteur du trapèze.

$$ \frac{(a+c) \cdot h}{2} $$

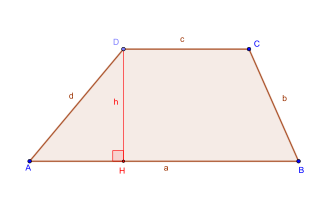
Pour le retrouver, vous pouvez calculer la hauteur des deux triangles sur les côtés et celle du rectangle “principal”, avant de les additionner.

Parmi les formules donnant les abscisses des points à considérer, on a donc prendre en compte les points au début et à la fin de chaque sous-intervalle.

Cela donne le code suivant, qui est très similaire à ce qu’on avait avant.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def calcul(f, a, b, n):
    somme = 0

    for k in range(n):
        somme += (
            f(a  + (b - a) * k / n) +
            f(a + (b - a) * (k + 1) / n)
        ) * (b - a) / (2 * n)

    return somme

Comme précédemment, plus $n$ est grand, meilleure la valeur est.

Méthode de Simpson

Cette méthode se distingue des précédentes par l’approximation utilisée : on ne passe pas par des approximations mettant en jeu des quadrilatères, mais des polynômes quadratique (de degré deux). Polynômes dont on sait facilement calculer l’intégrale !

Considérons en effet le polynôme suivant $$ P(X) = aX^2 + bX + c $$ Son intégration^[1] est directe :

$$ \int_a^b (at^2+bt+c)dt = \left[\frac{a}{3}t^3 + \frac{b}{2}t^2 + ct \right]_a^b $$

Formule de Newton-Cotes

On approximait précédemment notre intégrale par une suite de polynôme de degré deux se succédant. Qu’en est-il de l’approximer directement sur l’intervale entier avec un unique polynôme.

L’approche connue sous le nom de Newton-Cotes met donc à l’oeuvre une interpolation polynomiale pour calculer l’aire de l’intégrale.

Intégrales et séries

Ce passage est destiné à des lecteurs plus avertis, ayant des rudiments sur les notions de séries.

En effet, on a la proposition suivante.

De plus, pour une application k-lipschitzienne, la différence entre les deux termes est en $O(\frac{1}{n})$.

Ce n’est pas tout de l’affirmer, prouvons le !

Note de l’auteur : on pourrait également aborder les méthode de Boole-Villarceau ainsi que Weedle-Hardy, qui correspondent pour l’essentiel aux formules de Newton-Cotes avec des polynôme de degré respectifs quatre et six.