Toujours garder en tête la courbe du sinus et du cosinus !
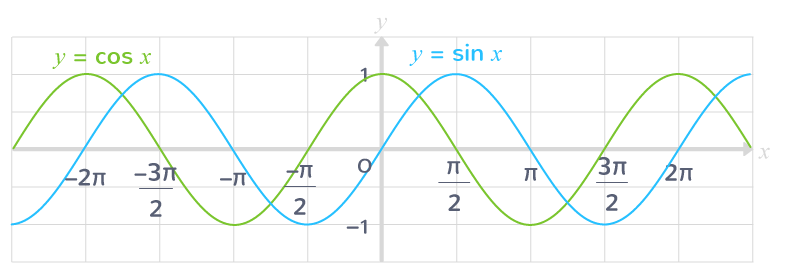
De plus, il est primordial ne pas oublier le cercle trigonométrique : le cosinus est le projeté sur l’axe des abscisses, et le sinus le projeté sur l’axe des ordonnées !
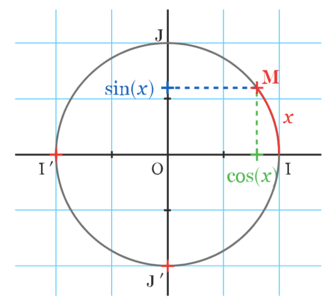
Sur ce schéma, la tangente est l’intersection entre la droite OM et la droite verticale passant pas I.
Relations fondamentales
$$ \tan(x) = \frac{\sin(x)}{\cos(x)} $$
$$ \cos^2(x) + \sin^2(x) = 1 $$
Périodicité
$$ \sin(2\pi + x) = \sin(x) $$ $$ \cos(2\pi + x) = \cos(x) $$ $$ \tan(2\pi + x) = \tan(x) $$
Parité
$$ \sin(-x) = - \sin(x) $$ $$ \cos(-x) = \cos(x) $$ $$ \tan(-x) = - \tan(x) $$
Vocabulaire
On dit que le cosinus est une fonction paire alors que le sinus et la tangente sont des fonctions impaires.
Une fonction f est paire si pour tout $x$, $$ f(-x) = f(x) $$ et impaire si pour tout $x$, $$ f(-x) = - f(x) $$
Valeurs remarquables
| x | $\sin(x)$ | $\cos(x)$ | $\tan(x)$ | $\text{cotan}(x)$ |
|---|---|---|---|---|
| 0 | $0$ | $1$ | $0$ | Non défini |
| $\frac{\pi}{6}$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{3}$ | $\sqrt{3}$ |
| $\frac{\pi}{4}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $1$ | $1$ |
| $\frac{\pi}{3}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\sqrt{3}$ | $\frac{\sqrt{3}}{3}$ |
| $\frac{\pi}{2}$ | $1$ | $0$ | Non défini | $0$ |
| $\pi$ | $0$ | $-1$ | $0$ | Non défini |
Comment le retenir ?
Ces valeurs ne sont pas aussi saugrenues qu’elles le paraissent quand on regarde le cercle trigonométrique !
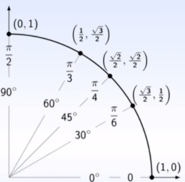Pour le retenir, une technique est d’inscrire dans le sens croissant les valeurs 1, 2, 3 sur l’axe des abscisses de 0 à 1, de prendre leurs racines carrées puis de tout diviser par 2 !
Tu remarqueras que ce sont les valeurs prises par le cosinus pour respectivement $\frac{\pi}{3}$, $\frac{\pi}{4}$ et $\frac{\pi}{6}$ radians.
On peut faire pareil vers le haut pour le sinus !
Transformations remarquables
Première transformation en $\pi - x$.
$$ \sin(\pi - x) = \sin(x) $$ $$ \cos(\pi - x) = - \cos(x) $$ $$ \tan(\pi - x) = - \tan(x) $$
Deuxième transformation en $\pi + x$.
$$ \sin(\pi + x) = - \sin(x) $$ $$ \cos(\pi + x) = - \cos(x) $$ $$ \tan(\pi + x) = \tan(x) $$
Troisième transformation en $\frac{\pi}{2} - x$.
$$ \sin(\frac{\pi}{2} - x) = \cos(x) $$ $$ \cos(\frac{\pi}{2} - x) = \sin(x) $$ $$ \tan(\frac{\pi}{2} - x) = \frac{1}{\tan(x)} $$
Quatrième transformation en $\frac{\pi}{2} + x$.
$$ \sin(\frac{\pi}{2} + x) = \cos(x) $$ $$ \cos(\frac{\pi}{2} + x) = - \sin(x) $$ $$ \tan(\frac{\pi}{2} + x) = - \frac{1}{\tan(x)} $$
Cinquième transformation en $\frac{3\pi}{2} - x$.
$$ \sin(\frac{3\pi}{2} - x) = - \cos(x) $$ $$ \cos(\frac{3\pi}{2} - x) = - \sin(x) $$ $$ \tan(\frac{3\pi}{2} - x) = \frac{1}{\tan(x)} $$
Sixième transformation en $\frac{3\pi}{2} + x$.
$$ \sin(\frac{3\pi}{2} + x) = - \cos(x) $$ $$ \cos(\frac{3\pi}{2} + x) = \sin(x) $$ $$ \tan(\frac{3\pi}{2} + x) = - \frac{1}{\tan(x)} $$
Formules d’addition
$$ \sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b) $$ $$ \sin(a-b) = \sin(a)\cos(b) - \cos(a)\sin(b) $$ $$ \cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b) $$ $$ \cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b) $$ $$ \tan(a+b) = \frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)} $$ $$ \tan(a-b) = \frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)} $$
Comment le retenir ?
En réalité, seulement une formule suffit pour chaque fonction trigonométrique : l’autre peut se déduire grâce à la parité ou l’imparité de ces fonctions.
On peut aussi n’en retenir qu’une seule, pour retrouver les autres à partir des transformations remarquables.
En fin de compte, c’est surtout avec la pratique qu’elles se retiennent !
$$ \cos(p) + \cos(q) = 2 \cos\left(\frac{p+q}{2}\right) \cos\left(\frac{p-q}{2}\right) $$ $$ \cos(p) - \cos(q) = - 2 \sin\left(\frac{p+q}{2}\right) \sin\left(\frac{p-q}{2}\right) $$ $$ \sin(p) + \sin(q) = 2 \sin\left(\frac{p+q}{2}\right) \cos\left(\frac{p-q}{2}\right) $$ $$ \sin(p) - \sin(q) = 2 \cos\left(\frac{p+q}{2}\right) \sin\left(\frac{p-q}{2}\right) $$ $$ \tan(p) + \tan(q) = \frac{\sin(p+q)}{\cos(p) \cos(q)} $$ $$ \tan(p) - \tan(q) = \frac{\sin(p-q)}{\cos(p) \cos(q)} $$
Comment le retenir ?
Je trouve celles-ci plus compliquées à retenir, un moyen mnémotechnique étant de se rappeler des formules d’additions précédente, pour ensuite réfléchir aux éléments qui se téléscoppent.
Un autre moyen pour retenir les quatre premières est “coco-moins-sisi-sico-cosi” dans l’ordre des formule.
$$ \sin(a)\sin(b) = \frac{1}{2}\left( \cos(a-b) - \cos(a+b) \right) $$ $$ \cos(a)\cos(b) = \frac{1}{2}\left( \cos(a+b) + \cos(a-b) \right) $$ $$ \sin(a)\cos(b) = \frac{1}{2}\left( \sin(a+b) + \sin(a-b) \right) $$
Comment le retenir ?
À vrai dire, ce sont surtout des reformulations de formules précédentes…
Formules de duplication
$$ \sin(2a) = 2 \sin(a) \cos(a) $$ $$ \cos(2a) = \cos^2(a) - \sin^2(a) \ = 2 \cos^2(a) - 1 \ = 1 - 2 \sin^2(a) $$ $$ \tan(2a) = \frac{2\tan(a)}{1 - \tan^2(a)} $$
Comment le retenir ?
Ce sont des formules d’addition abbrégées !!!
Formules de linéarisation
$$ \sin^2(a) = \frac{1 - \cos(2a)}{2} $$ $$ \cos^2(a) = \frac{1 + \cos(2a)}{2} $$ $$ \tan^2(a) = \frac{1 - \cos(2a)}{1 + \cos(2a)} $$
Comment le retenir ?
Elle viennent des différentes expressions de $\cos(2a)$
$$ \cos^3(a) = \frac{\cos(3a) + 3\cos(a)}{4} $$ $$ \sin^3(a) = \frac{- \sin(3a) + 3\sin(a)}{4} $$ $$ \tan^3(a) = \frac{- \sin(3a) + 3\sin(a)}{\cos(3a) + 3\cos(a)} $$
Formules de l’angle moitié
On pose $t = \tan(\frac{a}{2})$. On a alors
$$ \sin(a) = \frac{2t}{1 + t^2} $$ $$ \cos(a) = \frac{1 - t^2}{1 + t^2} $$ $$ \tan(a) = \frac{2t}{1 - t^2} $$
Expression par la tangente
$$ \sin^2(x) = \frac{\tan^2(x)}{1 + \tan^2(x)} $$ $$ \cos^2(x) = \frac{1}{1 + \tan^2(x)} $$
Formule de Moivre
Pour $n \in \mathbb{N}$, $$ (\cos(a) + i \sin(a))^n = \cos(na) + i \sin(na) $$
Formules d’Euler
$$ \cos(\theta) = \frac{e^{i\theta} + e^{-i\theta}}{2} $$ $$ \sin(\theta) = \frac{e^{i\theta} - e^{-i\theta}}{2} $$
Dérivées
$$ \cos’(x) = - \sin(x) $$ $$ \sin’(x) = \cos(x) $$
Comment le retenir ?
Pour trouver la dérivée avec le signe, il faut parcourir le cercle trigonométrique dans le sens horaire en regardant les directions où on lit la valeur du sinus et du cosinus.
La dérivée du sinus est le cosinus, et celle du cosinus est l’opposé du sinus, et ainsi de suite…
Éléments de preuve
J’ai écrit pêle-mêle des éléments de preuve et les idées principales que j’utilise pour retenir l’origine des formules. Ce ne sont donc pas des démonstrations rigoureuses 😉
Transformations remarquables
Pour la première transformation $\pi - x$, les angles sont symétriques par rapport à l’axe des ordonnées (axe vertical des y). La lecture des valeurs sur le cercle trigonométrique suffit en tenant compte de la parité.
Pour la deuxième transformation $\pi + x$, on a des angles alternes-internes et la lecture sur le cercle trigonométrique en tenant compte de la parité suffit aussi.
Pour la troisième transformation $\frac{\pi}{2} - x$, c’est comme si le cercle trigonométrique avait subi une rotation de $\frac{pi}{2}$ radians dans le sens horaire, et qu’on lisait les valeurs “à l’envers”. EN faisant cela on a en quelque sorte “inversé” le cosinus et le sinus.
La quatrième transformation $\frac{\pi}{2} + x$ peut être vue similairement, mais la parité vient jouer des tours…
Concernant la cinquième $\frac{3\pi}{2} - x$ et la sixième $\frac{3\pi}{2} +x$, ce sont à peu près les même que les deux d’avant, au facteur devant $\pi$ près. Elles sont juste un peu plus tordues.
Formules d’additions
On va utiliser le produit scalaire dans le cercle trigonométrique.
On prend deux vecteurs $\vec{u}$ et $\vec{v}$ tels que leurs normes soient égales à 1 et qu’ils décrivent des angles respectifs $a$ et $b$ par rapport à l’axe des abscisses.
Ce qui va suivre n’est pas compliqué, juste n’oubliez pas de faire un dessin pour bien comprendre ce qui se passe !
Leurs coordonnées dans le repère orthonormé usuel (habituel) sont donc :
$$ \vec{u} = \cos(a)\vec{u_x} + \sin(a)\vec{u_y} $$ $$ \vec{v} = \cos(b)\vec{u_x} + \sin(b)\vec{u_y} $$
Et l’angle (en conservant le signe donc dans le sens trigonométrique) entre les deux vecteurs est $$ (\vec{u}, \vec{v}) = a - b $$
On peut ensuite écrire leur produit scalaire de deux manières différentes.
$$ \vec{u} \cdot \vec{v} = \cos(\vec{u}, \vec{v}) = \cos(a)\cos(b) + \sin(a)\sin(b) $$
D’où
$$ \cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b) $$
Puis
$$ \cos(a+b) = \cos(a-(-b)) = \cos(a)\cos(-b) + \sin(a)\sin(-b) $$
Et la parité des fonctions fait le reste ! Pour ce qui est du sinus, on réalise les manipulations qui suivent.
$$ \sin(a-b) = \sin\left(\frac{\pi}{2} - (\frac{\pi}{2}-a+b)\right) = \cos\left((\frac{\pi}{2}-a)+b\right) $$
On utilise ensuite la formule d’addition du cosinus, puis celles de transformations pour arriver à $\cos(a)$ et $\sin(a)$, et la parité pour calculer $\sin(a+b)$, comme pour le cosinus.
La tangente s’obtient de la manière qui suit :
- On utilise la forme explicite puis les formules d’addition du cosinus et du sinus. $$ \tan(a+b) = \frac{\sin(a+b)}{\cos(a+b)} = \frac{\sin(a)\cos(b) + \cos(a)\sin(b)}{\cos(a)\cos(b) - \sin(a)\sin(b)} $$
- On divise tout par $\cos(a)\cos(b)$ $$ \tan(a+b) = \frac{\frac{\sin(a)}{\cos(a)} + \frac{\sin(b)}{\cos(b)}}{1 - \frac{\sin(a)\sin(b)}{\cos(a)\cos(b)}} = \frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)} $$
Comme avant, $\tan(a-b)$ s’obtient par parité à partir de $\tan(a+b)$.
Pour toutes les formules qui suivent, il faut poser $p = a + b$ et $q = a - b$, ce qui donne $a = \frac{p+q}{2}$ et $b=\frac{p-q}{2}$. Avec les formules d’addition du cosinus et du sinus on arrive aux formes souhaitées qui se téléscoppent gentimment.
On les manipule légèremment pour les trois dernières.
Formules de duplication
Les formules de duplication viennent des formules d’addition. $$ \sin(2a) = \sin(a+a) = 2 \sin(a) \cos(a) $$
Et on bidouille $$ \cos(2a) = \cos(a+a) = \cos^2(a) - \sin^2(a) $$ Avec $$ \cos^2(a) + \sin^2(a) = 1 $$
Formules de linéarisation
On trouve par les formules de duplication $$ \cos(2a) = 2\cos^2(a) - 1 = 1 - \sin^2(a) $$
Et les formules voulue s’obtiennent à partir de cela, pour $\tan^(a)$ on substitue le sinus et cosinus.
Formules de l’angle moitié
Expression par la tangente
$$ \cos^2(x) = \frac{\cos^2(x)}{\cos^2(x) + \sin^2(x)} = \frac{1}{1 + \frac{\sin^2(x)}{\cos^2(x)}} = \frac{1}{1 + \tan^2(x)} $$
$$ \sin^2(x) = \frac{\sin^2(x)}{\cos^2(x) + \sin^2(x)} = \frac{\frac{\sin^2(x)}{\cos^2(x)}}{1 + \frac{\sin^2(x)}{\cos^2(x)}} = \frac{\tan^2(x)}{1 + \tan^2(x)} $$
Formules de Moivre
Il faut utiliser l’exponentielle complexe :
$$ (\cos(a)+i\sin(a))^n = (e^{ia})^n = e^{ian} = \cos(na)+i\sin(na) $$
Formules d’Euler
On utiise de nouveau l’exponentielle complexe.
$$ \frac{e^{ia}+e^{-ia}}{2} = \frac{2\cos(a)}{2} = \cos(a) $$ $$ \frac{e^{ia}-e^{-ia}}{2} = \frac{2\sin(a)}{2} = \sin(a) $$